它是一种表示法,决定算法运行的速度有多快或多慢。这个速度不是由秒决定的,而是由算法的运行时间随着元素的增加而增加多少决定的。
大o是时间和大小的关系。在整篇文章中,您将看到包含这些度量的图表,并且您将在实践中更好地理解它们。我们有两种类型的复杂性(空间和时间)。
时间复杂度: 确定执行与输入大小成正比的算法所需的时间。
空间复杂度: 确定将分配多少内存来查找我们需要的项目。
为什么要研究这个?
通过它,您可以确定算法的可扩展性 大o总是处理最坏的情况,例子如下:示例:
您有一个列表,并且想要搜索某个项目,但该项目位于列表的末尾。最坏的情况是你必须执行尽可能多的操作,直到找到你想要的数据。执行次数
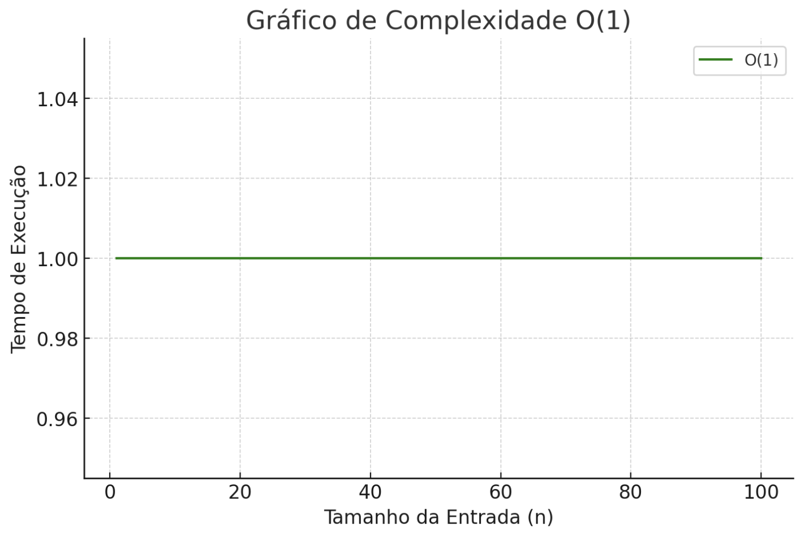
康斯坦特节奏 o(1):
无论数组大小如何,总是花费相同的时间示例:
增加或减少1
2
3
4
5
6
7
function increment(value: number){
return ++value
}
function decrement(value: number){
return --value
}
1
2
3
4
5
6
7
8
const fruits = ["apple", "orange", "grape", "banana"]
function getitem(items: string[], index: number) {
return items[index]
}
const item = getitem(fruits, 2)
console.log(`fruit: ${item}`) // "grape"
1
2
3
4
5
const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]
function getfirstelement(items: string[]){
return items[0]
}
1
2
3
4
5
6
7
8
const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]
function getlastelement(items: string[]){
return items[item.length - 1]
}
let lastelement = getlastelement(animes)
console.log(`last element: ${lastelement}`)
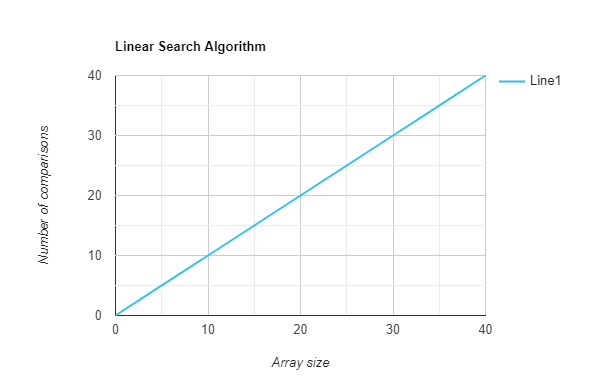
线性时间 o(n):
执行时间与数组大小成正比 排序和二分搜索算法 仅使用一个循环进行迭代示例:
为了找到 10 个项目的数组中最大的数字,我将滚动所有项目,直到找到它。 在最坏的情况下,最大的数字将是最后一个。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const numbers = [0, 4, 8, 2, 37, 11, 7, 48]
function getmaxvalue(items: number[]) {
let max = numbers[0];
for (let i=0; i <= items.length; i++){
if(items[i] > max) {
max = items[i]
}
}
return max;
}
let maxvalue = getmaxvalue(numbers)
console.log(`max value: ${maxvalue}`)
对数时间 o(log n)
输入大小增加n,执行时间增加log n,时间以对数比例增长。 记住 n 是数组中元素的数量。 输入的增长速度快于执行时间。 我们将在数组中执行二分搜索来查找特定项目。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const numbers = [0, 9, 24, 78, 54, 88, 92, 100, 21, 90]
function binarysearch(nums: number[], target: number) {
let left = 0;
let right = nums.length - 1;
while (left <= right) {
let middle = math.floor((right + left) / 2);
if (nums[middle] === target) {
return middle;
} else if (nums[middle] < target) {
left = middle + 1;
} else {
right = middle - 1;
}
}
return -1;
}
let gettarget = binarysearch(numbers, 92)
console.log(`target: ${gettarget}`)
log2(10) = 3.4
log2(20) = 4.3
log2(40) = 5.3 下面的图表将更容易理解: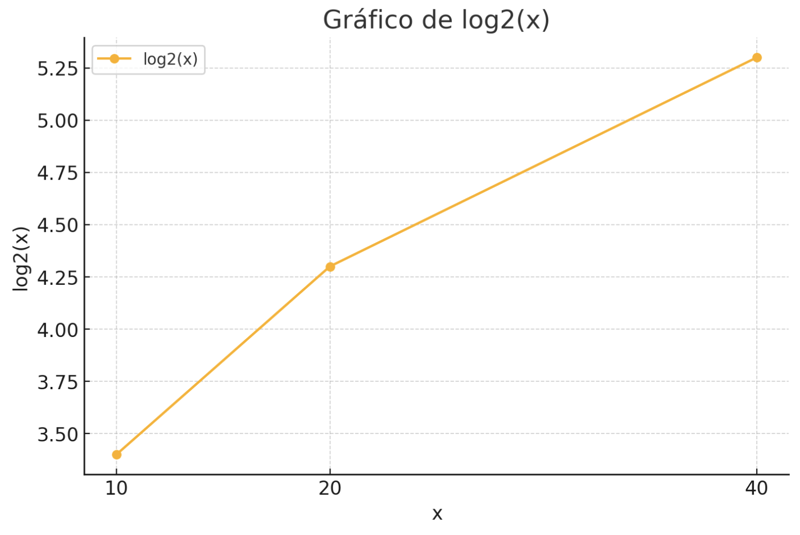
线性/拟线性时间 o(n log n)
算法的时间复杂度是指执行n次对数运算。 o(log(n)) 和 o(n) 的混合。 归并排序就是一个结构示例。 适度增长。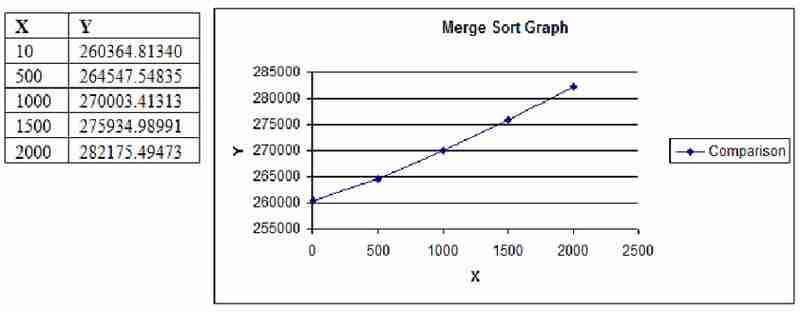
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
function merge(arr, left, middle, right) {
const leftarraysize = middle - left + 1;
const rightarraysize = right - middle;
const leftarray = new array(leftarraysize);
const rightarray = new array(rightarraysize);
for (let i = 0; i < leftarraysize; i++) {
leftarray[i] = arr[left + i];
}
for (let j = 0; j < rightarraysize; j++) {
rightarray[j] = arr[middle + 1 + j];
}
let i = 0;
let j = 0;
let k = left;
while (i < leftarraysize && j < rightarraysize) {
if (leftarray[i] <= rightarray[j]) {
arr[k] = leftarray[i];
i++;
} else {
arr[k] = rightarray[j];
j++;
}
k++;
}
while (i < leftarraysize) {
arr[k] = leftarray[i];
i++;
k++;
}
while (j < rightarraysize) {
arr[k] = rightarray[j];
j++;
k++;
}
}
function mergesort(arr, left = 0, right = arr.length - 1) {
if (left < right) {
const middle = math.floor((left + right) / 2);
mergesort(arr, left, middle);
mergesort(arr, middle + 1, right);
merge(arr, left, middle, right);
}
return arr;
}
function testmergesort() {
const arr1 = [64, 34, 25, 12, 22, 11, 90];
console.log("sorted array:", mergesort([...arr1]));
}
testmergesort();
二次时间 o(n²)
随着输入数量的增加,执行时间呈二次方增加。 阅读矩阵。 基本上当需要 2 个嵌套循环时 冒泡排序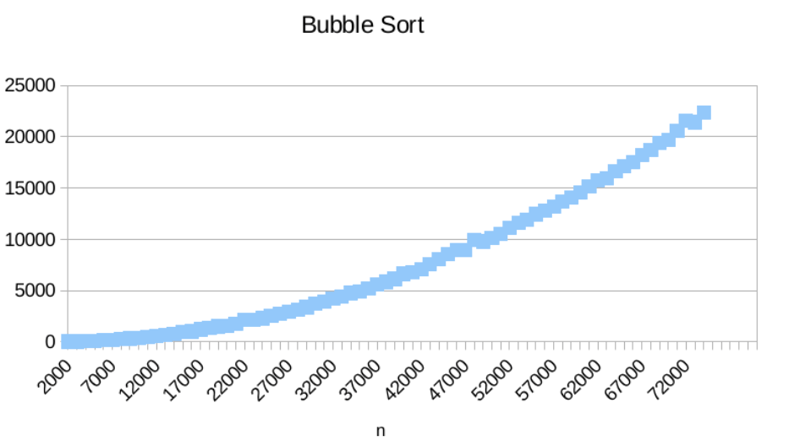
示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
function creatematrix() {
const matrix = [
[2,4,5,],
[89,0,12],
[13,76,89]
];
for (let i = 0; i < matrix.length; i++) {
for (let j = 0; j < matrix[i].length; j++) {
console.log(`element at [${i}][${j}]: ${matrix[i][j]}`);
}
}
}
时间指数 o(2ˆn)
每插入一个元素到输入中,执行时间就会加倍。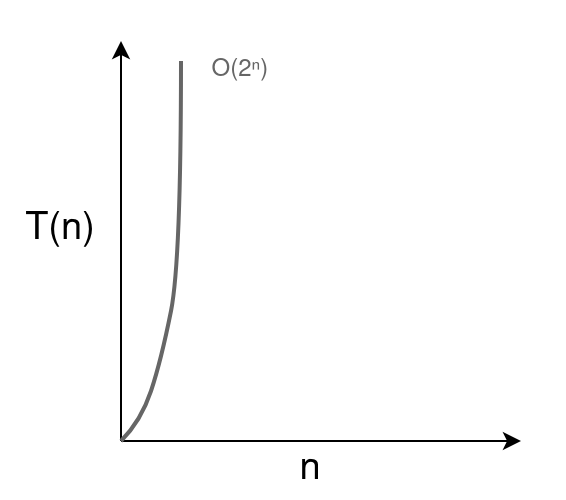
1
2
3
4
5
6
7
function fibonacci(n) {
if(n <= 1){
return n
} else {
return fibonacci(n-1) + fibonacci(n-2)
}
}
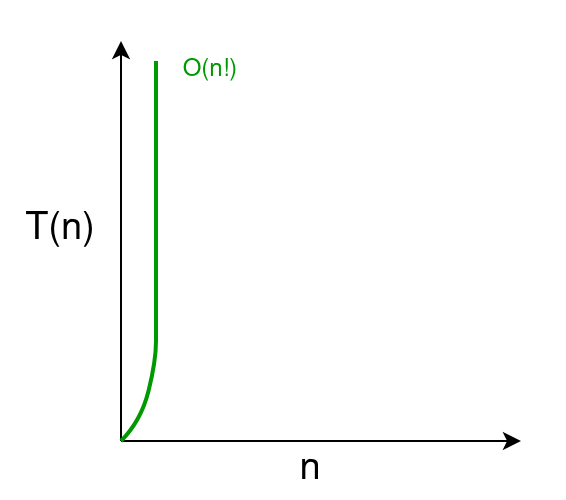
阶乘时间 o(n!)
执行时间根据输入的大小按阶乘增加。示例:
生成数组内的所有排列1
2
3
4
5
6
7
8
9
10
11
12
13
function factorialIterative(n) {
if (n === 0 || n === 1) {
return 1;
}
let result = 1;
for (let i = 2; i <= n; i++) {
result *= i;
}
return result;
}
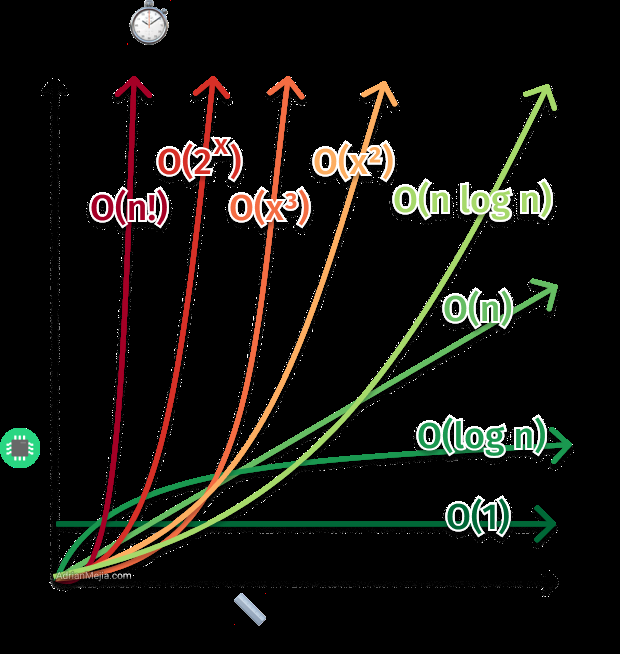
以上就是大 O 符号的详细内容,更多请关注php中文网其它相关文章!

